jlearner

JLearner Exercises

For each exercise, write some assert statements that check that your solution works correctly. For example:

Declarations:

int sum(int x, int y) {
  return x + y;
}

Statements:

assert sum(3, 4) == 7;
assert sum(1, 2) == 3;

If you want to easily copy-paste all of your code into and out of JLearner in one step, write your statements inside a main method:

Declarations:

int sum(int x, int y) { return x + y; }
void main() {
  assert sum(3, 4) == 7;
  assert sum(1, 2) == 3;
}

Expression: main()

Note: all Java language constructs that you need to use for these exercises are also used in the examples that you can find via the drop-down menu at the top of the JLearner webpage, so you may want to open a second copy of JLearner in a separate window so that you can look at a relevant example while making an exercise.

Note: some later exercises build on earlier ones, so keep your solutions.

Methods, loops

Declare a method that computes the sum of three given integers.
Declare a method that computes the average (rounded toward zero) of two given integers (Note: in Java, if x and y are of type int, x / y is the quotient of x and y, rounded toward zero.)
Declare a method that computes the absolute value of a given integer.
Declare a method that computes the minimum of two given integers.
Declare a method that computes the minimum of three given integers.
Declare a method that computes x to the power of y, for nonnegative y (iterative implementation)
Declare a method that computes x to the power of y, for nonnegative y (recursive implementation)
Declare a method that computes the square root (rounded down) of a given nonnegative integer. (Find the largest integer whose square is not greater than the given number, by simply trying all integers, starting from zero, and going up. So: start at zero and check if the square of the next bigger integer would be greater than the given number. If so, you have found the square root, rounded down. If not, try the next bigger integer.)

Arrays

Declare a method that counts the number of zeroes in a given array
Declare a method that replaces each element in an array by its negation
Declare a method that returns a new array whose elements are the negation of the elements of a given array

Objects

Declare a class Vector such that an object of this class can be used to store a two-dimensional vector with integer coordinates x and y. (That is, declare a class Vector with a field x and a field y.)
Declare a method that returns the magnitude (also known as the Euclidian length) (rounded down) of the vector stored in a given Vector object. (Use the square root method you declared earlier.)
Declare a method that returns whether the vector stored in one given Vector object is larger than the vector stored in another given Vector object. Use the size method you declared in the previous exercise.
Declare a method that returns a new Vector object that stores the sum of the vectors stored in two given Vector objects.
Declare a method that translates (shifts) the vector stored in a given Vector object by the vector stored in another given Vector object. It updates the first Vector object; it does not create a new object.

Siblings

A person is a sibling of another person if they are either a brother or a sister of the other person. For these exercises, assume no two siblings have the same age.

Declare a class such that an object of this class can be used to store the age and the next oldest sibling of a person. (That is, declare a class Person with a field age and a field nextOldestSibling.) (The next oldest sibling of a person is the oldest sibling of that person that is younger than that person.) If a person has no younger siblings, store null in the corresponding nextOldestSibling field.
Declare a method that counts the number of younger siblings of some person, given a Person object corresponding to that person (iterative implementation).
Declare a method that counts the number of younger siblings of some person, given a Person object corresponding to that person (recursive implementation).
Declare a method that returns an array containing the younger siblings of some person, given a Person object corresponding to that person (iterative implementation).
Declare a method that counts the number of adult younger siblings of a some person, given a Person object corresponding to that person (iterative implementation).
Declare a method that counts the number of adult younger siblings of a some person, given a Person object corresponding to that person (recursive implementation).
Declare a method that increments the age stored for some person, as well the ages stored for the person's younger siblings by one, given a Person object corresponding to that person (iterative implementation).
Declare a method that increments the age stored for some person, as well the ages stored for the person's younger siblings by one, given a Person object corresponding to that person (recursive implementation).
Declare a method that updates the Person object corresponding to the youngest sibling of some person p to reflect the fact that a new sibling (age 0) was born, given a Person object corresponding to person p (iterative implementation).
Declare a method that updates the Person object corresponding to the youngest sibling of some person p to reflect the fact that a new sibling (age 0) was born, given a Person object corresponding to person p (recursive implementation).

Arrays of vectors

Declare a method that, given an array of vectors, returns the sum of the vectors (i.e. a vector whose X coordinate is the sum of the X coordinates of the given vectors, and whose Y coordinate is the sum of the Y coordinates of the given vectors).
Declare a method that, given an X value and an array of vectors, returns the Y coordinate of some vector in the array whose X value equals the given X value, or 0 if there is no such vector in the array.
Declare a method that, given an array of vectors, returns a new array that contains the same Vector objects, but in reverse order. That is, the last element of the given array should be the first element of the returned array, etc. Do not modify the given array or the vectors.
Declare a method that, given an array of vectors, reverses it in-place. That is, swap the first and the last vector, the second and the second-but-last, etc. This method shall not return anything; it should be a void method.
Declare a method that, given a vector and an array of vectors, replaces each vector in the array whose X and Y coordinates are equal to those of the given vector by the given vector.

Marriage

Declare a class Person with a field spouse that can refer to a Person object.
Declare a method that, given a Person object and an array of Person objects, returns the number of occurrences of the given Person object in the array.
Declare a method that, given an array of Person objects, checks that no Person object occurs more than once in this array.
Declare a method that, given an array of Person objects, checks for every person P in the array that if P is married to P', then P' is in the array and is married to P, and no person is married to themselves.
Declare a method that, given an array of Person objects, replaces each married person in the array by their spouse. Check that applying this method to an array twice restores the array to its original state.
Declare a method that, given an array of an even number of distinct Person objects (i.e. no Person object occurs more than once in the array), marries all unmarried persons.

One-way streets

Declare a class Crossroads with a field outgoingRoads that can point to an array of Crossroads objects.
Declare a method that, given a Crossroads object and an array of N Crossroads objects, returns an array of length N+1 that contains the elements of the given array followed by the given Crossroads object.
Declare a method that, given an integer N and two Crossroads objects, checks whether the second Crossroads object can be reached from the first Crossroads object by following an outgoing road at most N times. In other words, check whether there is a path of length at most N that starts at the first Crossroads object and ends at the second Crossroads object. (Hint: use recursion.)
Declare a method that, given an integer N and a Crossroads object, checks whether the given Crossroads object can be reached from itself by following an outgoing road at most N times. In other words, check whether there is a path of length at least 1 and at most N that starts and ends at the given Crossroads.
Declare a method that, given a Crossroads object, returns an array of Crossroads objects that contains each Crossroads object reachable from the given Crossroads object (including the given Crossroads object itself) exactly once. (Hint: use recursion.)
Declare a method that checks that a given array of Crossroads objects is closed, meaning that any Crossroads object reachable from an object in the array is also in the array.
Declare a method that, given a closed array of Crossroads objects, returns an array of Crossroads objects representing the inverted road network. That is, the returned array shall be such that, for every pair of indices I and J, if the Crossroads object at index I in the original array has an outgoing road to the Crossroads object at index J in the original array, then the Crossroads object at index J in the returned array shall have an outgoing road to the Crossroads object at index I in the returned array.
Declare a method that, given two Crossroads objects, checks that the two road networks reachable from them are isomorphic. This means that for each Crossroads object reachable from the first given Crossroads object, there exists a corresponding Crossroads object reachable from the second given Crossroads object such that if a Crossroads object O reachable from the first given Crossroads object has an outgoing road to some Crossroads object O', then the object corresponding to O has an outgoing road to the object corresponding to O', and vice versa.

Sorting

Checks

Declare a method isSorted such that isSorted(array) returns true if and only if the values stored in array are stored in ascending order, i.e. for any two indices I and J, if I < J then array[I] <= array[j].
Declare a method that counts the number of occurrences of a given value in a given array.
Declare a method that returns whether an array is a permutation of another array. This is the case if the arrays have the same length and for each element of the first array, the number of occurrences of that element in the first array equals the number of occurrences of that element in the second array.
Declare a method that returns whether an array is a sorted version of another array.

Insertion sort

Declare a method insert such that insert(array, n, v) inserts value v into the sorted sequence of values stored at indices 0 (inclusive) through n (exclusive) of array, such that afterwards, the sequence of values stored at indices 0 (inclusive) through n + 1 (exclusive) is sorted. You will need to shift the elements of the sequence that are greater than v one position to the right. You may assume that the given array has length n + 1 or greater.
Declare a method insertionSort such that insertionSort(array) replaces the sequence of values stored in array with a sorted version of that sequence. Hint: first use insert to insert the second element into the sequence at indices 0 (inclusive) through 1 (exclusive). Then use insert to insert the third element into the sequence at indices 0 (inclusive) through 2 (exclusive). And so on.

Selection sort

Declare a method removeGreatest such that removeGreatest(array, n) returns the greatest element of the sequence of values stored at indices 0 (inclusive) through n (exclusive) in array, and removes one occurrence of that element from the sequence. You will need to shift the elements that appear after the removed element to the left by one position.
Declare a method selectionSort such that selectionSort(array) replaces the sequence of values stored in array with a sorted version of that sequence. Hint: first use removeGreatest to remove the greatest element of the sequence and then put that element in the last position. Then use removeGreatest to remove the greatest element of the remaining sequence and then put that element in the one-but-last position. And so on.

Merge sort

Declare a method merge such that merge(array1, array2) returns an array that satisfies the following properties:
- for each value V, the number of occurrences of V in the result array equals the number of occurrences of V in array1 plus the number of occurrences of V in array2
- if array1 and array2 are sorted (i.e. the elements in the array are stored in ascending order), then the result array is sorted as well.
Declare a method subarray such that subarray(array, a, b) returns an array of length b - a that contains the elements at indices a (inclusive) through b (exclusive) of array.
Declare a method mergeSort such that mergeSort(array) returns a new array that stores the sequence of values obtained by sorting the sequence of values stored in array. Hint: if the length of the array is 0 or 1, just return a copy of the array. Otherwise, use subarray to get the two halves of array, sort them using a recursive call of mergeSort, and then merge them using merge.

Heap sort

In computer science, a tree consists of a number of nodes. Each node has zero or more children, which are themselves nodes. Each node is a child of at most one other node, which is called its parent. Exactly one node has no parent; this node is called the root node of the tree. We say the tree is rooted in that node.

A binary tree is a tree where each node has at most two children.

We can interpret an array as a binary tree as follows:

Each array element is a node.
The element at index 0 is the root node.
The parent node of the element at index N + 1 is the element at index N/2. This means that the children of the root node are at indices 1 and 2, the children of the node at index 1 are at indices 3 and 4, the children of the node at index 2 are at indices 5 and 6, the children of the node at index 3 are at indices 7 and 8, etc.

We say a tree is a max-heap if the value of a node is not less than the values of its children. In a max-heap, the value of the root node is the maximum value of all nodes of the tree.

Given a max-heap with N nodes in an array of length N + 1 or greater, we can add an element to the heap by first putting it at index N, i.e., by adding it as a child of the node at index (N-1)/2. Notice that this may break the max-heap property: the new value might be greater than its parent's value. If so, we swap the two values. But then, if the parent node is not the root node, the max-heap property may still be broken because the parent node's value might be greater than its own parent node's value. So we apply this sift up operation recursively to fully restore the max-heap property.

Declare a method heapAdd(array, n) that adds the element at index n to the heap at indices 0 (inclusive) through n (exclusive), using the sift up algorithm.

Given a max-heap with N nodes, we can remove the root element by replacing it with the value of the leaf node at index N-1. At this point, the max-heap property may be broken because the new root value might be less than the value of one (or both) of the root node's children. In that case, we swap the root node's value with that of the child with the greatest value. But then, if this child has children of its own, the max-heap property may still be broken since this child's value may now be less than that of one (or both) of its own children. Therefore, we recursively apply this sift down operation to the child.

Declare a method heapRemove(array, n) that removes the root element (i.e. the greatest element) of the heap at indices 0 (inclusive) through n (exclusive) and returns its value.

We can turn an array into a max-heap (known as heapification) as follows:

Notice, first, that the heap consisting only of the node at index 0 is automatically a max-heap.
We can add each next element of the array to the heap using the heapAdd method defined above.

We can sort an array by first heapifying it and then repeatedly removing the greatest element and putting it in the space freed.

Declare a method heapSort such that heapSort(array) sorts array using this heap sort algorithm.

Search tree

A search tree is an ordered tree: the order of the children of a given node is important. Specifically, in a search tree, if child A is before child B, then the values stored in the subtree rooted at child A are less than the values stored in the subtree rooted at child B.

Declare a class TreeNode that represents a node in a search tree. Each node stores a reference to its first child node (or null if it has no children), its next sibling node (or null if it has no further siblings), and its value. The children of a node are the first child and the first child's siblings.
Declare a method that counts the number of children of a given node.
Declare a method that returns an array containing the sequence of children of a given node.
A node is called a leaf if it has no children. Declare a method that counts the number of descendants of a given node that are leaves. (Hint: use recursion.)
Declare a method addLeafValues(node, array, i) that writes the values of the descendants of node that are leaves into array starting at index i and returns the number of values written. (Hint: use recursion.)
Declare a method that returns an array containing the values of the descendants of a given node that are leaves. One can think of the tree rooted in the given node as storing this set of values.
Declare a method that checks that the values of all descendants of a given node that are leaves are less than or equal to a given value.
Declare a method that checks that for each descendant D of a given node that has a next sibling, the values of the descendants of D that are leaves are less than or equal to the value of D. In this case, we say the tree is valid. We say a node is an interior node if it is not a leaf. The value of an interior node that has a next sibling serves as an upper bound on the values stored by the tree rooted in that node. (The value of an interior node that does not have a next sibling has no meaning.)
A sequence of trees is called a forest. The sequence of the children of a given node is, in particular, a forest. Declare a method that returns whether a given value is the value of a leaf in the forest rooted at a given node. Use the values of the interior nodes for performance. Specifically:
- If the given node is a null reference, return false.
- If the given node is a leaf:
  - If the given value is less than the node's value, return false.
  - If the given value equals the node's value, return true.
  - If the given value is greater than the node's value, recursively check the node's next sibling.
- If the given node is not a leaf:
  - If the given node does not have a next sibling or the given value is not greater than the node's value, recursively check the node's first child.
  - If the given node has a next sibling and the given value is greater than the node's value, recursively check the node's next sibling.
Declare a method that adds a given value to the forest rooted in a given node and returns the new root node. Specifically:
- If the given node is a null reference (i.e. we are adding a value to an empty forest), create a new leaf node whose value is the given value and return it.
- If the given node is a leaf:
  - If the given value is less than the node's value, create a new node with the given value as its value and the given node as its next sibling, and return the new node.
  - If the given value equals the node's value, simply return the given node. (The tree already contains the value, so no modifications are required.)
  - If the given value is greater than the node's value, recursively add the given value to the given node's next sibling, set the given node's next sibling reference to the return value, and return the given node.
- If the given node is not a leaf:
  - If the given node does not have a next sibling or the given value is not greater than the node's value, recursively add the given value to the given node's first child, set the given node's first child reference to the return value, and return the given node.
  - If the given node has a next sibling and the given value is greater than the node's value, recursively add the given value to the given node's next sibling, set the given node's next sibling reference to the return value, and return the given node.
Declare a method that removes a given value from the forest rooted in a given node and returns the new root node.

Example

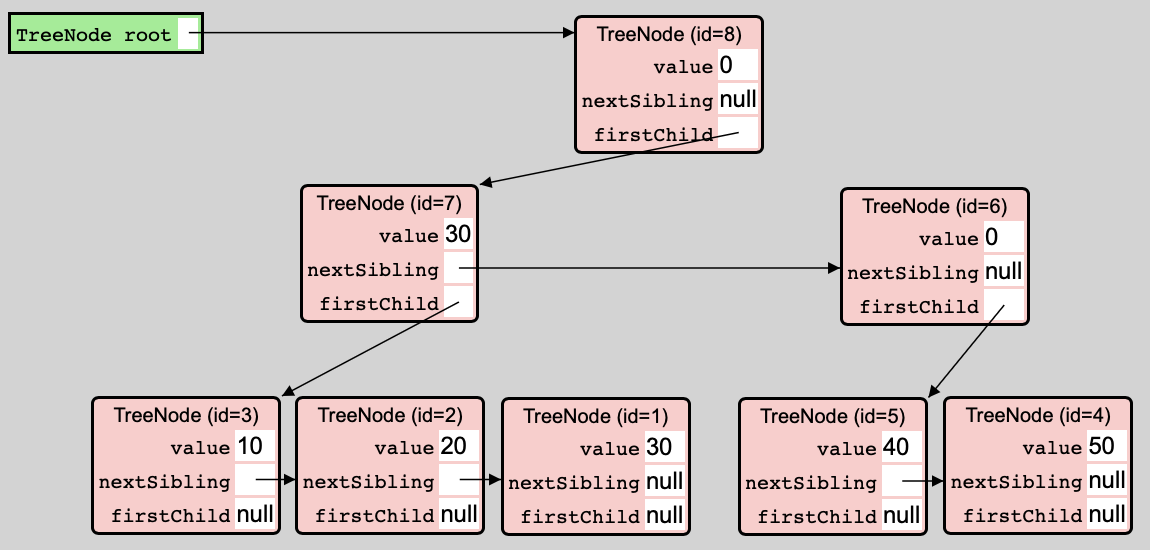
A search tree

Consider the example tree shown above. The node id=8 has two children: id=7 and id=6. Node id=7 itself has three children: id=3, id=2, and id=1. Node id=6 has two children: id=5 and id=4. All nodes besides id=8 are descendants of id=8. The leaf nodes are id=3, id=2, id=1, id=5, and id=4. The interior nodes are id=8, id=7, and id=6.

This tree is a search tree: the values 10, 20, 30 stored in the subtree rooted at id=7 are less than the values 40, 50 stored in the subtree rooted at id=6. The search tree is valid: the value 30 of interior node id=7 is an upper bound for the values 10, 20, 30 stored by the subtree rooted in that node. The values of interior nodes id=8 and id=6 have no meaning because they have no next sibling.

Balanced search tree

Declare a method that returns the maximum of the two given numbers.
Declare a method that returns the height of the forest rooted in a given node. The height of a null pointer is zero. The height of a node is the maximum of one more than the height of the forest rooted in its first child and the height of its next sibling.
Declare a method that returns whether a given forest is perfectly balanced. This is the case when each tree has the same height, and furthermore each tree's sequence of children is itself perfectly balanced.
Declare a method that returns whether a given forest is two-three; this means that each interior node has either two or three children. An interior node with less than two children is called light, and a node with more than three children is called heavy.
Declare a method that adds a given value to the forest rooted in a given node, while ensuring that if the forest was two-three before, it will again be two-three afterwards. Specifically, if after the operation, a tree has four children, replace it with two trees of two children. (Notice that this method does not change the height of the forest.)
Declare a method that adds a given value to the forest rooted in a given node, while ensuring that if the forest was two-three and had at most three trees before, it will again be two-three and have at most three trees afterwards. Specifically, if the forest has four trees, combine the trees to create two higher trees. (Notice that this operation may change the height of the forest.)
Declare a method that removes a given value from the forest rooted in a given node, while ensuring that if the forest was two-three before, it will again be two-three afterwards. Specifically, if after the operation, a tree has only one child, merge it with a sibling to obtain either two trees of two children (if the sibling had three children) or one tree with three children (if the sibling had two children). (Notice that this operation does not change the height of the forest.)
Declare a method that removes a given value from the forest rooted in a given node, while ensuring that if the forest was two-three before, it will again be two-three afterwards and furthermore, if it has only one tree, that tree is a leaf. Specifically, if after the operation, there is only one tree, replace it with its children. (Notice that this operation may change the height of the forest.)

The example tree shown above is perfectly balanced and two-three.

Notice that if a forest is two-three and has at most three trees, then checking whether the forest has a leaf with a given value, adding a given value, and removing a given value take time proportional to the height of the forest in the worst case. Furthermore, if the forest is perfectly balanced as well, the number of leaves in the forest is at least 2^(H-1) (rounded down), where H is the height of the forest, or, in other words, the height of the forest is at most the 2-logarithm of the number of leaves plus 1. That means that the lookup, add, and remove operations take time logarithmic in the number of leaves.